Depth First Search for Hard Sudoku

Badri Toppur, TAPMI, Manipal

badri.toppur@gmail.com

This paper demonstrates an implementation of depth first search (DFS) to fill all the empty cells in the sudoku grid correctly. There are easy versions with dense matrices, hard versions that are sparse matrices, and in the worst case is the blank matrix. We present a scheme that is based up on keeping track of ones guesses . This is complemented by a finite set of principles for testing whether a row, column or subsquare is complete without duplication of a digit. Whenever one encounters infeasibility due to cell assignments following a guess, or a sequence of consecutive guesses, one takes back all the temporary cell assignments up to the previous guess and trys an alternative spot for the guess in the same subsquare or try a new digit in a new subsquare.

The completed sudoku solution reveals an immediate application as a set covering problem in which there are n² job categories with n² persons in each category and 3n² districts that need to share these human resources. The sudoku solution is the assignment with the best utilization, such that no two workers are assigned the same job and no two jobs are assigned to the same worker.

1. Introduction

Sudoku a game based upon a grid, appeared first as Number Place in 1979 in “Dell Pencil Puzzles and Word Games” magazine and is attributed to Howard Garns [2]. In the eighties it became popular in Japan under its current name. It then spread to Great Britain and finally the rest of the world. It features a 9´ 9 square matrix much like a crossword grid. This square is divided into nine equal sub-squares. Using the numbers from 1 to 9 one must fill in all the squares so that none of the nine subsquares, or the nine rows or the nine columns have a digit appearing more than once. On the other hand each digit must appear in each subsquare, row and column at least once.

2. Strategy for Easy Sudoku

I	II	III
IV	V	VI
VII	VIII	IX

Figure 1 Numbering the sub-squares Figure 2 The puzzle

A simple strategy exists for solving the easy version of this game. Suppose the nine subsquares are numbered from left to right from the top as in Figure 1. Focus on three subsquares in a row or in a column. These will be made up of three rows or three columns depending on which manner we pick the three 3 ´ 3 subsquares. Suppose we pick the three subsquares on the top of the grid. Scanning the three topmost rows in Figure 2 one can see there is the digit ‘4’ in each of the three rows. They are in different rows and not confronting each other. There is the digit ‘9’ in the second subsquare and a ‘9’ in the third subsquare, but there is no ‘9’ in the first subsquare. So we can conclude that a ‘9’ is required in the first subsquare. Furthermore it cannot be in the second or third row, but must be in the first row given the object of the game. The first row in subsquare I has two empty cells and an ‘8’ in the third cell. Into which cell will we place the ‘9’? Looking down the first column one can see a ‘9’ in the first cell in subsquare IV, so this rules out the first square. Therefore the ‘9’ must go into the second cell of subsquare I. Now we know where the ‘9’ is in the first subsquare.

Looking down the first three columns, that is subsquares I, IV, and VII; there is a ‘9’ missing in the seventh subsquare. Where does the ‘9’ go in this subsquare? One can get a clue from the ‘9’ that we have just entered in subsquare 1, and the ‘9’ in the eight subsquare. To avoid the ‘9’ in seventh row, and the two ‘9’s in the first two columns, we have to put the ‘9’ in the eight row to the right of the ‘6’ in subsquare VII.

If one is unable to make headway with the ‘9’ then try another number. If all the remaining numbers fail to pin any new entries, move to a new row or column of subsquares. After a few permanent assignments one can return to ‘9’ or whichever number one began with.

In more complex versions of the game, there are usually too few numbers provided for one to obtain the complete solution using just the above strategy. One needs to take guess at certain points to get ahead at all. Typically there one to three choices for a particular digit in a subsquare. After making one of these choices, one keeps assigning temporary labels from this point onwards. If no contradiction is reached, and one reaches the limits of deduction based upon that guess, we take another guess, and continue the process. If a contradiction to the rules is observed one has to undo all the temporary labels and make another choice for that particular digit.

Thus we need to keep track of the sequence of guesses, and also the sequence of temporary cell assignments that make up each guess, so that we can backtrack to the position in the decision tree, where we may have chosen unwisely. To each digit entered whose status is temporary, one needs a subscript indicating its position in the sequence of temporary cell assignments made in the current drive. What if a second guess is required. One needs a superscript to keep track of the guess number. If we realize that we have made a mistake in the cell assignments, we can backtrack with the aid of this subscript and superscript. Permanent cell assignments are distinguished by the absence of these subscripts or superscripts. Book-keeping also has to include the coordinates of the cell for the guesses, to avoid repetition after back-tracking. All this information is maintained separately in appropriate data structures.

3. Depth First Search for Hard Sudoku

We have presented a labelling scheme with temporary and permanent cell assignments with descent down a search tree, with branching nodes denoting multiple conditional guesses about the cell assignment of a particular digit. This descent is followed by backtracking back up to the root node, whenever one encounters infeasibility, i.e. a contradiction between the temporary cell assignment and some previous temporary or permanent cell assignment. We present an example in this section and dozens more in the appendix. In terms of computational time and other performance measures these are to be used to empirically determine heuristic rules for deciding which digit to branch upon and in which subsquare to place the digit.

Example 1

2				5			8
			8		4
4					7	5
		3	6			8
8			7		2			9
		6			5	4
		5	9					7
			4		1
	4			6				1

2				5	6		8	4
5			8		4
4			2		7	5
		3	6	4	9	8		5
8	5	4	7		2			9
		6		8	5	4
		5	9	2			4	7
			4	7	1		5	8
	4		5	6				1

Figure 3 HARD 9´ 9 problem Figure 4 Without Guesswork

Consider the puzzle in Figure 3. One can without much look ahead and without any guesswork get to the position indicated in Figure 4. An automated procedure, that in the absence of robotic vision, necessarily proceeds in the dark, will require a labelling scheme from the very first square that is filled regardless of how obvious things are by inspection. At this stage, one must take a guess. One can take a guess about any digit missing in some subsquare. A guess that helps clear some of the congestion of blank cells is preferable, to one that is appears ornamental. In an automated search procedure, the multiplicity of guesses corresponding to such entries that do not quickly help one locate other digits is not appear to be a critical factor.

2	6^212		3^210	5	6		8	4
5	3^211		8		4
4	8^11		2		7	5
1^26	7^25	3	6	4	9	8	2^23	5
8	5	4	7		2			9
9^22	2^21	6	1^28	8	5	4	7^24	3^29
	1^27	5	9	2	8^13		4	7
			4	7	1		5	8
7^15	4	8^12	5	6	3^14			1

Figure 5

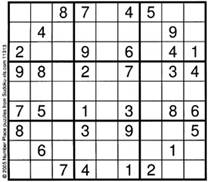
The first guess in this example is in the third row and second column of subsquare I as in Figure 5: The digit ‘8’ is definitely required in the third row. The two choices are cell (3, 2) and (3,3), either one of them will be denoted 8¹₁ to indicate that this is the first entry in the sequence corresponding to the first guess. Conditional to this guess, one can deduce another four digits in sequence, upto the cell in the ninth row and first column: 7¹₅. This is the end of the run of deductions based upon this guess. One must guess again, and the second guess is about the location of the digit ‘2’ in subsquare IV. There are again two choices for this ‘2’. It must go into cell (4,2) or (6,2). Let us go with the guess that the ideal position for the ‘2’ designated as 2²₁ is in the cell (6, 2). In the run of logical deductions that follow, one can go up to eleven more guesses before placing a temporary ‘6’ in the same row as a permanently placed ‘6’. These twelve temporary entries are also indicated in Figure 5. We next roll back the last twelve temporary labels constituting the second guess, and take another branch at the first position. Recall that our alternate choice for the position of the digit ‘2’ is in the cell (4,2). We get up to 1²₈ in cell (7,2) with no contradiction. This leads to a third guess starting arbitrarily in the seventh row and first column about the digit ‘3’. This chain of deductions leads to two sixes in the seventh column as apparent in Figure 6, contradicting the rules of the puzzle.

2	3^35		1^38	5	6		8	4
5	6^35		8		4
4	8^11		2		7	5
1^24	2^21	3	6	4	9	8	7^23	5
8	5	4	7	1^37	2	6^310	1^39	9
9^26	7^25	6	3^36	8	5	4
3^31	1^28	5	9	2	8^13	6^34	4	7
6^33	9^27	2^22	4	7	1	3^32	5	8
7^15	4	8^12	5	6	3^14			1

Figure 6

We therefore roll back all the moves from the third guess and try the only other possible location for the three in subsquare VII, that is in cell (8,1). This leads to the situation depicted in Figure 7.

2				5	6		8	4
5			8		4
4	8^11		2		7	5
1^24	2^21	3	6	4	9	8	7^23	5
8	5	4	7		2			9
9^26	7^25	6		8	5	4
6^32	1^28	5	9	2	8^13	3^34	4	7
3^31	9^27	2^22	4	7	1	6^33	5	8
7^15	4	8^12	5	6	3^14			1

Figure 7

We require a fourth guess here. If we try 3⁴₁ in cell (6, 4) in subsquare V, we soon reach a contradiction in column seven with the digit ‘6’.

2				5	6		8	4
5			8		4
4	8^11		2		7	5
1^24	2^21	3	6	4	9	8	7^23	5
8	5	4	7	1^43	2	6^44	3^42	9
9^26	7^25	6	3^41	8	5	4
6^32	1^28	5	9	2	8^13	3^34	4	7
3^31	9^27	2^22	4	7	1	6^33	5	8
7^15	4	8^12	5	6	3^14			1

Figure 8

We can try putting this ‘3’ of the fourth guess in cell (5, 5).

2	6^45		3^43	5	6		8	4
5	3^44		8		4
4	8^11		2		7	5
1^24	2^21	3	6	4	9	8	7^23	5
8	5	4	7	3^41	2			9
9^26	7^25	6	1^42	8	5	4
6^32	1^28	5	9	2	8^13	3^34	4	7
3^31	9^27	2^22	4	7	1	6^33	5	8
7^15	4	8^12	5	6	3^14			1

Figure 9

This also leads to a contradiction. We have explored every node on this branch of the tree. Thus our very first placement of ‘8’ in cell (3,2) of subsquare I (Figure 5) is improper. The only alternative in this case is to place the very first ‘8’ in cell (3,3) in subsquare I as shown in Figure 11. We therefore take the other branch right at the start of the search and place the digit ‘8’ in cell (3,3), leaving us with the digits 1, 2, 3, 6, 7 and 9 that need to be filled in. Let the second guess be about the position of digit ‘1’ being in cell (6,2) in subsquare IV, also shown in Figure 10.

2			1^25	5	6		8	4
5		1^26	8		4
4		8^11	2		7	5		1^27
		3	6	4	9	8	1^23	5
8	5	4	7	1^22	2		6^17	9
	1^21	6	3^24	8	5	4
1^15	8^12	5	9	2	3^14	6^16	4	7
			4	7	1		5	8
	4		5	6	8^13			1

Figure 10

The two ‘1’s in the last column are a contradiction. So we take back the second guess about the position about the ‘1’ in subsquare IV, instead putting the 1²₁ in cell (4,2). This leads to the completion of the puzzle as seen in Figure 11. The depth first search tree is displayed in Figure 12.

2	7^223	1^228	3^211	5	6	9^225	8	4
5	6^222	9^227	8	1^230	4	7^224	3^232	2^220
4	3^226	8^11	2	9^229	7	5	1^231	6^221
7^24	1^21	3	6	4	9	8	2^23	5
8	5	4	7	3^29	2	1^27	6^17	9
9^25	2^22	6	1^210	8	5	4	7^26	3^28
1^15	8^12	5	9	2	3^14	6^16	4	7
6^213	9^216	2^215	4	7	1	3^217	5	8
3^214	4	7^212	5	6	8^13	2^218	9^219	1

Figure 11

Figure 12

4. Inductive Argument for Higher Dimensional Sudoku

The same technique must work for 4´4, 9´9, 16´16, 25´25 and in general n²´n² sudoku instances. Figures 13 and 14 show an easy instance of the 4´4 case and its solution.

1		4
4
	4	2

1	2	3	4
4	3	2	1
3	4	1	2
2	1	4	3

Figure 13 Figure 14

5. A Possible Application

In Figure 15 there is an assignment of workers to jobs indicated by the numeral 1. Worker A is assigned to job 1, worker B is assigned to job 6, worker C is assigned to job 3 and so forth. This assigment is not unique, but if there is some cost implicit with assigning a particular worker to a particular job, there will be a unique or a handful of solutions.

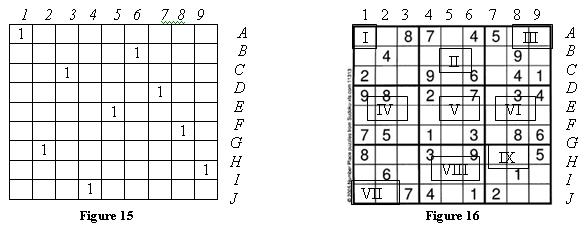
Returning to Su Do Ku - suppose we have 9 categories of jobs with 9 workers available in each category. Say these workers are – electrician (1), plumber (2), carpenter (3), mechanic (4), locksmith (5), doctor (6), cook (7), postman (8), and tailor (9). Furthermore suppose we want to assign these 81 workers to 27 villages in the district so that each village gets the services of each type of worker. These villages may be labelled A,….,J, 1,…,9 and I, …IX. In Figure 16, each row, each column and furthermore each of the nine sub-squares represents one village. Although it is a 2d grid one is thinking of three coordinates in this scheme. One can see that a number of assignments have already been made. For example village 1 has a designated plumber, a tailor, a cook and a postman. Village I has a designated plumber, a mechanic and a postman. One must simply fill in the remaining squares heeding the above mentioned restrictions on multiple assigments and absence of any assigments whatsoever.

6. References

[1] Will Shortz, 2005, “Sudoku – Easy to Hard”, Rupa and Co. Released originally by St. Martin’s Press, New York.

[2] R. E. Tarjan. 1983, “Data Structures and Network Algorithms”, Philadelphia, PA. Society for Industrial and Applied Mathematics. CBMS-NSF regional conference series in applied mathematics. Volume 44.